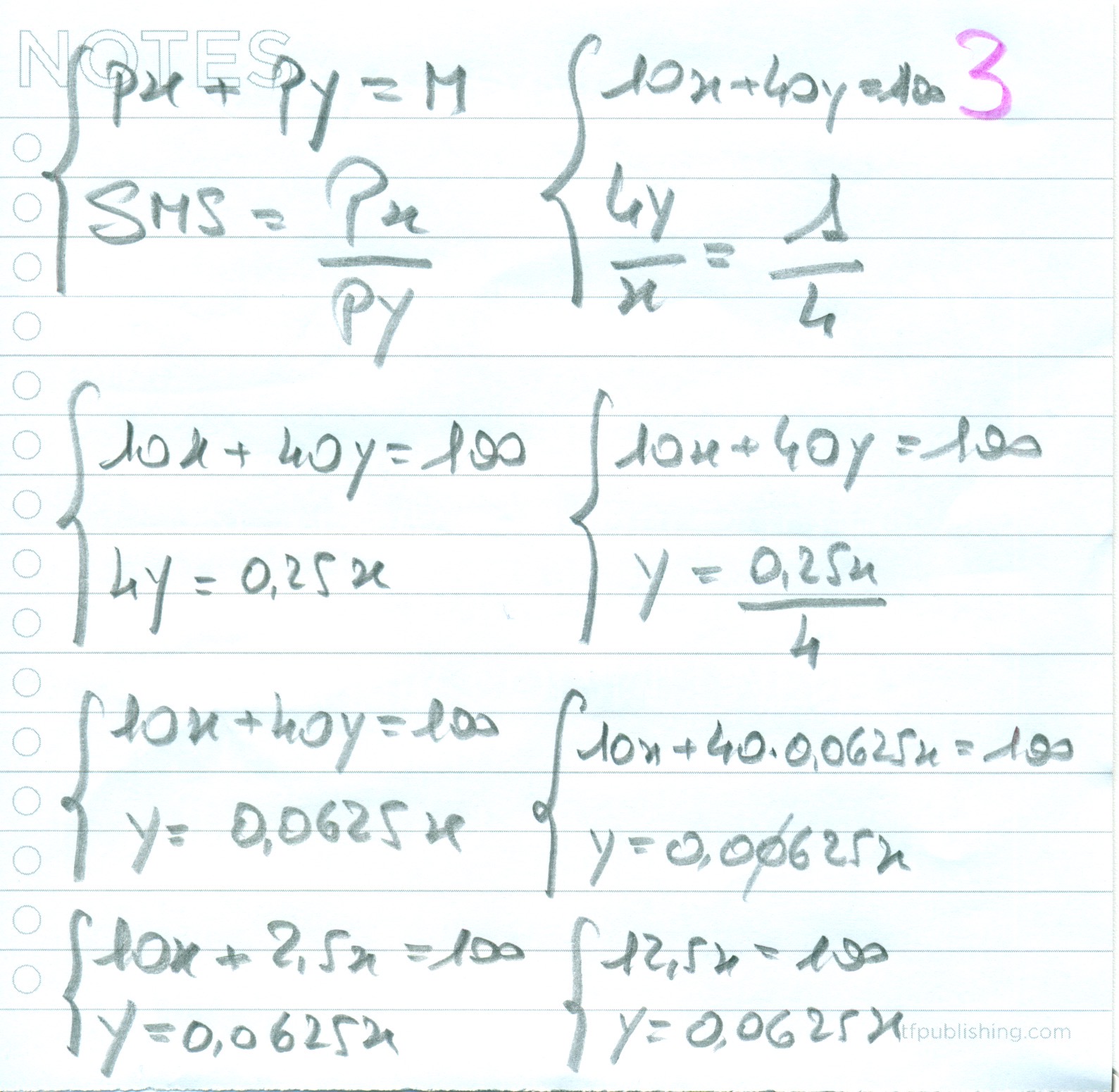Utilità, indicata con U = 2x alla 4° y.
Il prezzo di x è pari a 10 mentre quello di y è 40 con un reddito di 100.
Dati i prezzi, il reddito e l’utilità la domanda da porsi è:
- come disegnare il vincolo di bilancio con le annesse intercette d’ordinata e ascissa;
- calcolo del punto d’equilibrio tra il consumo di x e y.
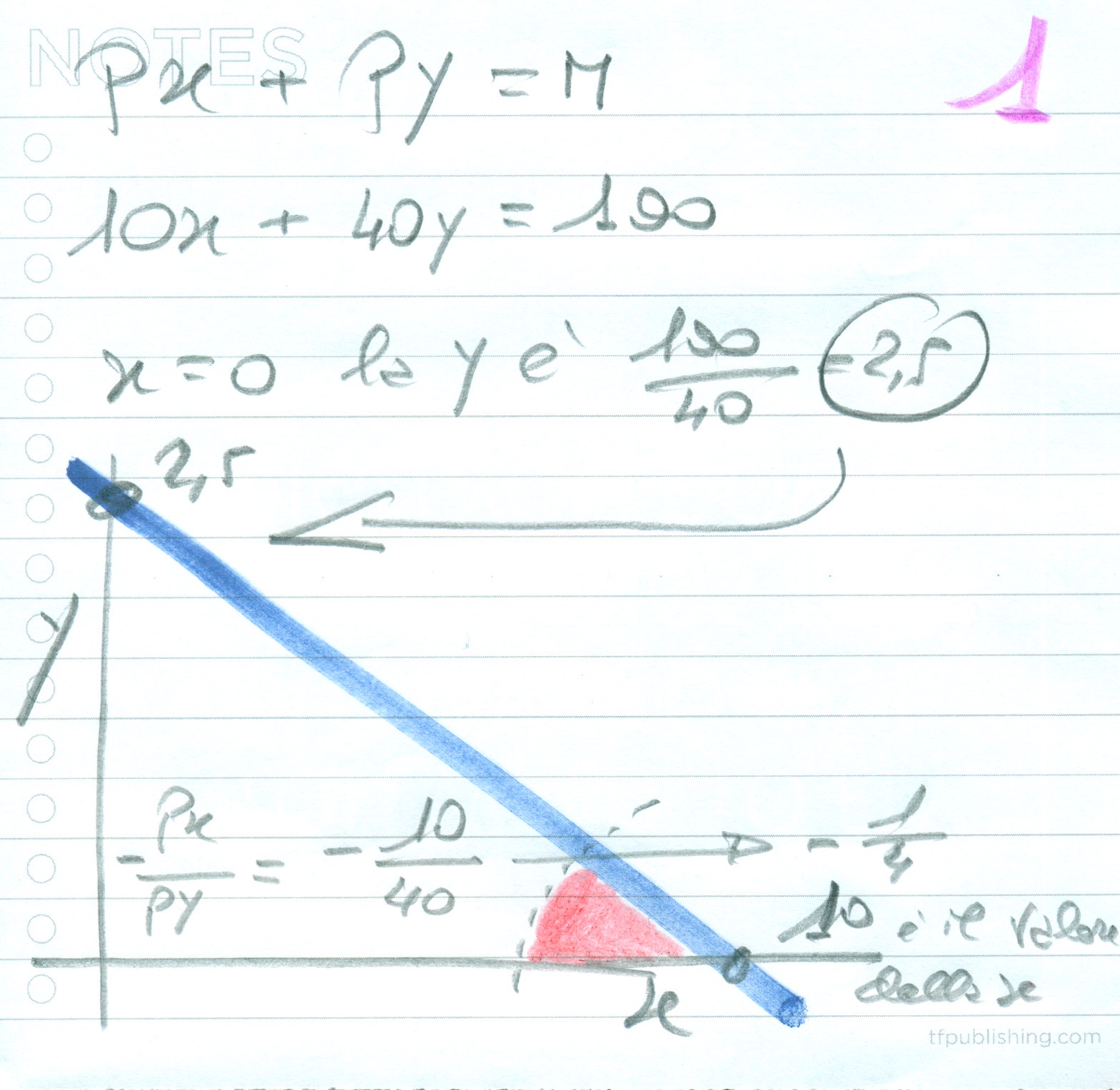
DETERMINAZIONE DEL VINCOLO DI BILANCIO (si veda grafica annessa – foglio 1)
Il vincolo di bilancio è pari a:
prezzo di x + prezzo di y = al reddito M
10x + 40y = 100
Il calcolo del vincolo di bilancio prevede che si ponga alternativamente a zero un’incognita per volta.
Posto x = 0 si ha:
10 per o è zero, quindi 40y = 100 consente di calcolare la y con 100/40 ovvero 2,5 (si veda grafica annessa)
Ponendo y = 0 ne consegue:
10x = 100 con la x pari a 10
ORA SI TRATTA DI CALCOLARE LA QUANTITA’ DI BENE X E Y CONSUMATA (si veda seconda grafica annessa – foglio 3 3/a)
Qui serve un sistema, ovvero una parentesi graffa che ponga in relazione sia il vincolo di bilancio sia il SMS (saggio marginale di sostituzione). Ecco pervenuti al punto più critico dell’intero problema, come s’ottiene il SMS?
Serve partire dalla funzione d’utilità, U = 2x elevato alla quarta e y. Per risolvere il problema della derivata parziale della funzione d’utilità (U) si veda un calcolo a parte (foglio allegato 2).
Ottenuto il SMS nei termini di 4y/x il conteggio prosegue come indicato nei fogli 3 e 3/a. Quindi nuovamente il vincolo di bilancio con curva d’indifferenza e quantificazione di consumo della x e della y.
Si noti il sistema (la graffa) che è “obbligatoria” quando si vuole calcolare la quantità consumata in presenza d’utilità, ovvero SMS e vincolo di bilancio: questo è il sistema di calcolo.
Ovviamente l’esercizio può essere complicato su diversi livelli ma già questo livello, da considerarsi semplice, rappresenta un buon esercizio per lo studente.
Buon studio