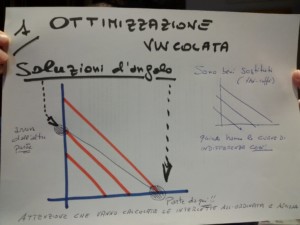
Soluzioni d’angolo intese come dettaglio di studio in microeconomia
Le soluzioni d’angolo rappresentano un concetto e un’eccezione precisa in microeconomia. Con quest’argomento si entra nella parte finale del programma per sostenere l’esame e passare a macro. Il guaio è che i diversi testi di microeconomia enunciano frettolosamente le soluzioni d’angolo, lasciando gli studenti a disagio nella comprensione.
Per capire le soluzioni d’angolo serve partire a monte dal concetto ottimizzazione vincolata. Si tratta di un “ambiente” dove ci sono 3 variabili da considerare. Il vincolo di bilancio, la curva d’indifferenza e il punto di contatto tra curva e vincolo. Esattamente in questo punto si ha l’uguaglianza tra il SMS (saggio marginale di sostituzione) e la pendenza del vincolo. Ovviamente questa uguaglianza viene espressa con dei simboli ben precisi.
Lo scopo della riflessione non è entrare in concorrenza con i sacri testi di microeconomia, quando spiegare ciò che è sottinteso.
Il SMS si riferisce alle UTILITA’ mentre sul vincolo di bilancio si discute tra beni e prezzi. Quest’ultimi sono “facilmente” identificati con delle coordinate. Al contrario l’utilità trovandosi su una curva d’indifferenza, obbliga all’uso della derivata.
Lo studio delle soluzioni d’angolo irrompe in questo bisogno d’uguaglianza per il punto d’ottimo. Si stabilisce così un altro equilibrio senza uguaglianza. La scelta ottima si colloca sull’ascissa o sull’ordinata (appunto all’angolo). Significa lanciare una retta tra 2 curve d’indifferenza cogliendo alternativamente un estremità con l’altra tra assi cartesiani. E’ saggio osservare il disegno qui indicato.
Il messaggio è chiaro. Non serve obbligatoriamente che ci sia l’uguaglianza tra SMS e inclinazione per assicurare un punto d’ottimo. Concretamente, per dare un’idea al tutto si sta parlando, ad esempio, di dolce o salato: gusti assoluti. In questo estremismo la soluzione è collocata all’angolo, appunto su un asse del piano cartesiano.
Seguono grafiche esplicative già note qui più evidenziate nei dettagli.