Saggio marginale di sostituzione come argomento abituale in questo sito dove la microeconomia impegna per un buon 20%.
Il restante si suddivide tra macro, un 10%, Ragioneria detta anche economia aziendale, un altro 20%, quindi considerazioni di fondo per un 30%.
Considerazioni di fondo che in realtà colgono molto spesso concetti di micro/macro. Infine la sociologia per il restante 20%.
Oggi qui affrontiamo una “grana” che deriva da un recente compito di microeconomia affrontato presso l’Università Cattolica di Milano.
Si noti l’allegato leggendo la prima parte, quella al punto 1 e la lettera “i”, l’ultimo quesito.

Lavorando sul punto “i” ci troviamo in una classica situazione d’elasticità unitaria.
Quella bisettrice che solitamente disegnano per trovare il punto ad elasticità unitaria ora è rappresentata dall’offerta.
Trovandosi l’offerta con intercetta nulla vuol dire che sorge dall’origine degli assi cartesiani. Sostanzialmente una situazione di questo tipo:
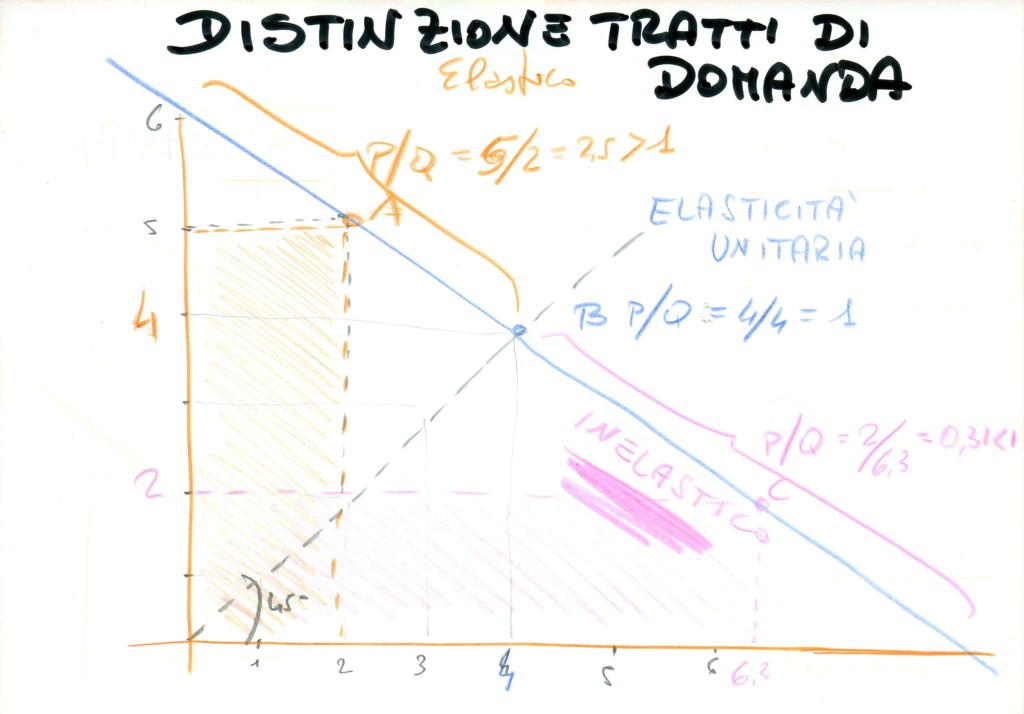
La soluzione al punto “i” quella ufficiale diffusa dall’Ateneo è la seguente:

Si noti come il prezzo d’equilibrio, quello che solitamente indichiamo con il p* asteriscato ci è dato, pari a 15.
Rapidamente otteniamo anche la q* in 40 unità. In questo modo ci troviamo ad avere quel p*/q* che ci serve per calcolare ogni elasticità.
Essendo la curva d’offerta Qs = 2p – 8 (si veda le istruzioni iniziali) noi calcoleremmo l’elasticità con un 2 (in negativo) che moltiplica p*/q*.
Il problema è però più complesso, noi sappiamo già che l’elasticità è pari a 1 (elasticità unitaria). Ne consegue che possiamo scrivere 1 = x per p*/q*.
Quel:
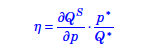
lo possiamo riscrivere in questo modo:

per risolverlo ci troviamo quel 15/40 invertito e moltiplicato avendo
Qs = 40/15p
infatti il testo indica 8/3 p perchè ha semplificato la funzione dividendo il numeratore e denominatore per 5 (15:5 = 3 e 40 : 5 = 8)
Chi non ha capito?
