Reddito e sostituzione effetti derivanti dalla variazione del prezzo. Parte 3°
Reddito e sostituzione sono i primi effetti studiati in microeconomia. Il passaggio è importante, perché si transita da un mondo “semplice” a quello in movimento. Concetti già espressi nella prima parte di trilogia dedicata all’effetto reddito e sostituzione.
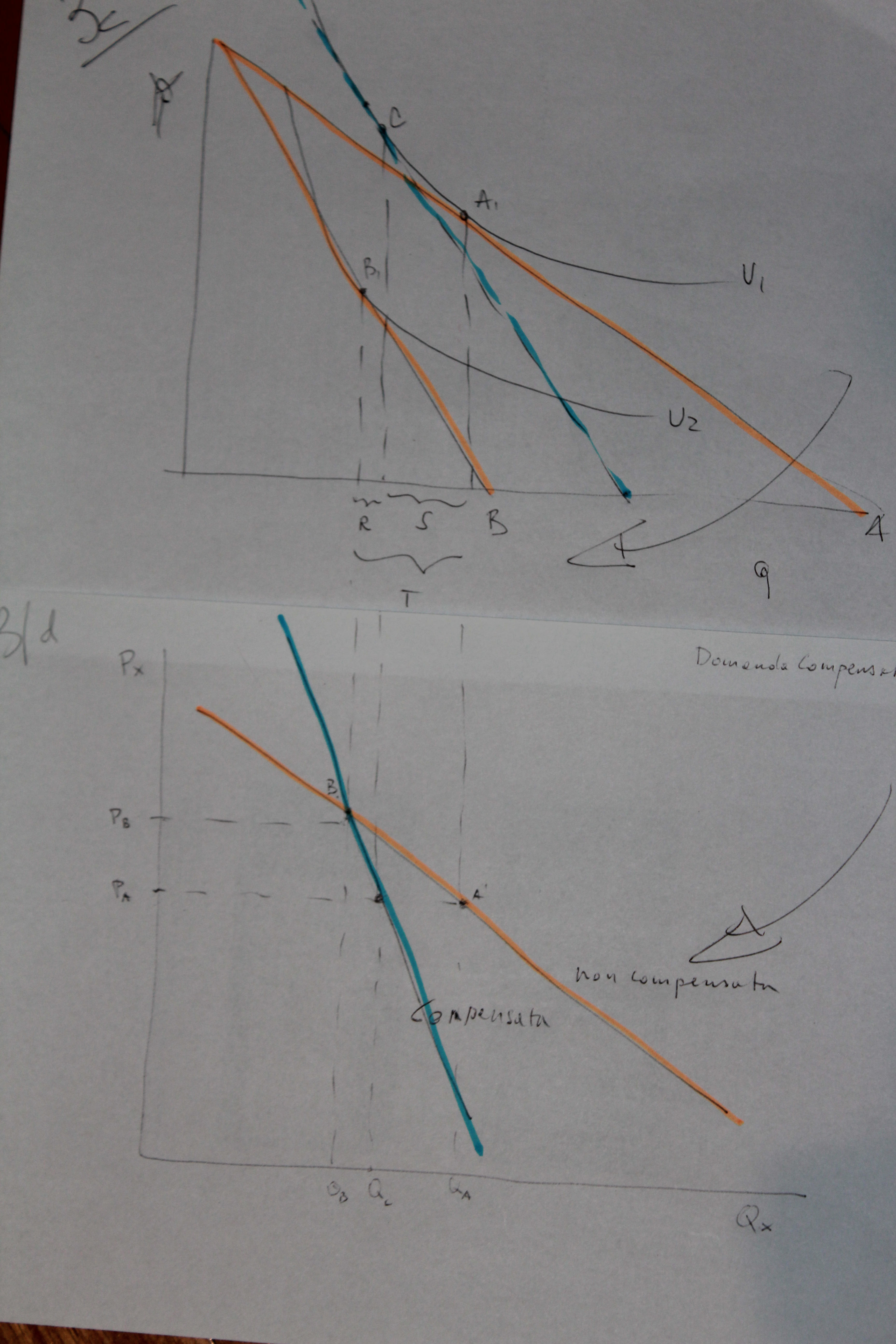
Nella seconda parte si è accennato al bisogno di riportare sul vincolo di bilancio opposto una parallela. Si è vero. Questa parallela serve per intercettare una diversa curva d’utilità. Nei disegni si chiama U1 e U2. Vediamo di capirci. Le curve chiamate “vincolo di bilancio” sono 2. Questo perché si parte da uno stadio e si perviene a un’altro. Ciò accade sia che il prezzo scenda o che ci sia un rincaro.
Assodato che le curve di bilancio sono 2, serve proiettare sull’altra la parallela di quella da cui si parte. In questo modo si riesce a trovare un terzo punto. Perchè terzo? è semplice. Il punto A è quello della prima curva di bilancio che interseca in funzione di ottimo paretiano la sua retta d’utilità (UT1). B è quel punto che vale tra la seconda retta di bilancio e l’altro ottimo paretiano su una diversa curva di utilità (UT2). Tutto ciò non basta, serve un punto C. Tale “C” si trova con la famosa parallela proiettata sul vincolo di bilancio opposto intersecando la curva di utilità lì presente. Evviva, ora abbiamo “C”.
L’effetto di reddito e sostituzione si calcola grazie ai punti A,B e C.
Non è finita. E’ necessario proiettare in basso, su altro grafico gli effetti di movimento tra vincoli di bilancio. Come visibile sull’immagine 3d si identifica una nuova dimensione. Si chiama curva compensata da contrapporre a quella non compensata. Un concetto di questo tipo ci apre alla curva di domanda classica e quella cosiddetta hicksiana. Quest’ultima esamina specificatamente l’effetto di sostituzione. Segue approfondimento sulla curva hicksiana.