Oligopolio come tortura segue a ben due studi pubblicati sul tema. In questa puntata si vuole sia esplorare il ruolo dei Ricavo marginale (RM) sia le curve di reazione quindi l’applicazione pratica.
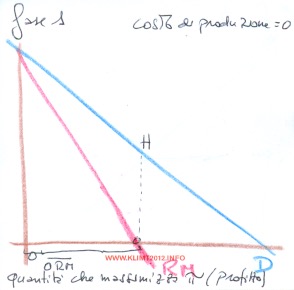
Applicando i concetti noti dal monopolio e considerando i costi marginali (CM) pari a zero, ovvero uguali all’ascissa, il mitico punto RC = CM si ha esattamente sull’ascissa. Si spera che la successione delle grafiche, qui offerte in visione, possa aiutare nella comprensione dell’oligopolio come tortura fino a questo punto.




Incamerati e capiti tutti i concetti espressi nei precedenti studi pubblicati, più quanto qui scritto, si passa a un altro concetto: le curve di reazione. Ecco dove l’oligopolio come tortura diventa concreto. E’ necessario capire dei concetti, quelli spiegati per sintetizzarli in una nuova dimensione dove le CURVE DI REAZIONE sono quanto stiamo cercando.
Il punto d’incontro tra le due curve di reazione è quello d’equilibrio, chiamato punto di Cournot.
La curva di reazione (detta anche curva di risposta ottima) rappresenta il comportamento ottimale di un’impresa preso atto dell’altro operatore di mercato. Questa curva è calcolata passando attraverso la massimizzazione del profitto della domanda residuale. Tradotto in termini concreti (si conferma l’oligopolio come tortura) si risolva il seguente esercizio.
Nell’immagine 1 il testo dell’esercizio e nella seconda la soluzione.


Per risolvere l’esercizio serve partire da una premessa. La Q è per tutto il mercato, ma le produzioni riguardano 2 imprese con qa + qb. Ne consegue che si legge p=100-Q ma si pronuncia p= 100 -qa – qb. Se non è stato chiarito questo passaggio non è possibile proseguire.
Chiarito il concetto ora si ragioni: il profitto d’impresa sarà pari al RT (ricavo totale) meno i CF (costi fissi) e i CV (costi variabili). In questo caso i CF sono pari a 100 e i CV in oligopolio sono pari al costo marginale, ovvero 10. Ne consegue che per calcolare il profitto dovremo fare RT – CT – CV (alias costo marginale).
Serve un terzo passaggio: per calcolare il Ricavo marginale serve la derivata prima della qa da cui emerge un 90 – 2qa- qb. Isolando qa si ottiene quel (90 – qb)/2 che va riportato nel grafico.
Anche sul grafico ci sono problemi, ma risolvibili. Per poter disegnare le curve basta porre a zero una delle due quantità agendo sull’altra. Ad esempio con qa=0 le intercette sono 45 e 90 e il contrario per la seconda curva di reazione.
ECCO COME SONO CALCOLATE LE CURVE DI REAZIONE!
