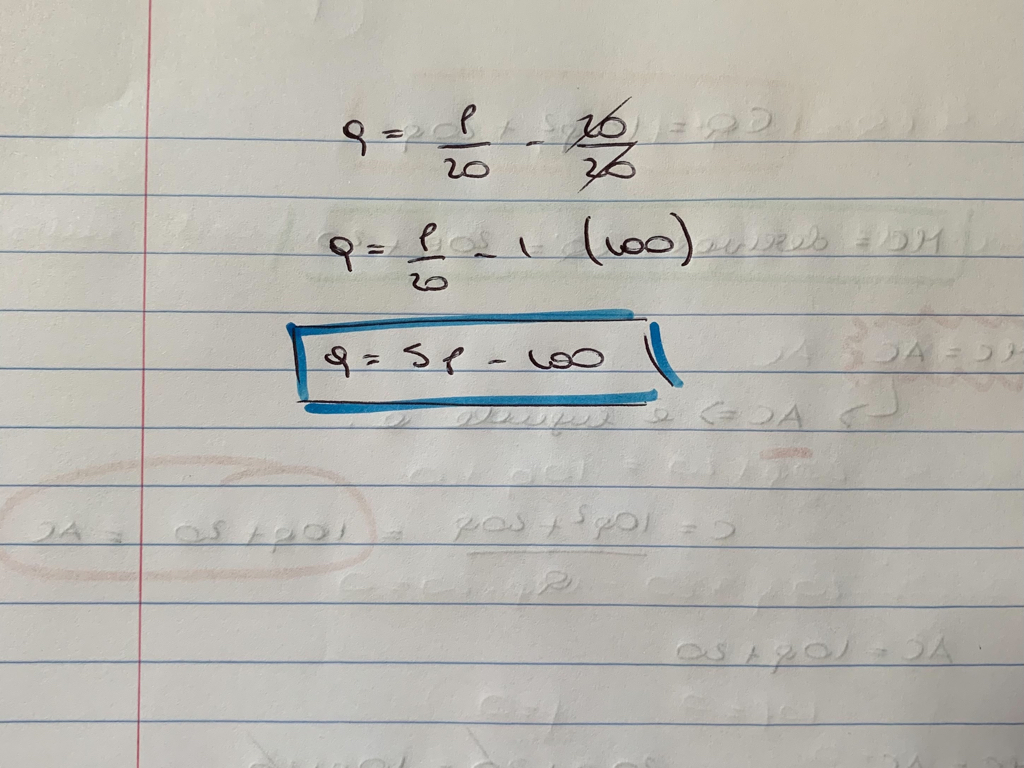Micro problema semplice ma blocca ogni studente ponendolo in difficoltà. Per questo motivo il Micro problema compare su queste pagine dove sono raccolte le maggiori sofferenze dei nostri ragazzi nelle materie che insegno.

Prima di tutto il tema (domanda 21 per punti 3)

Si consideri un mercato nel quale operano 100 imprese uguali che condividono tutte una funzione di costo totale di questo tipo, CT = 10q al quadrato + 20q. La curva d’offerta di mercato (valida per un prezzo superiore a 20) potrebbe essere definita tra una di queste 4:

Q = 2P

oppure Q = 50P -10

quindi Q = 5 + P/10

infine Q = -100 + 5P

Per risolvere il problema serve conoscere alcune regole.

La prima è che la curva del costo marginale identifica quella d’offerta nel tratto superiore al costo medio. Per spiegarsi è bene osservare la grafica qui predisposta:

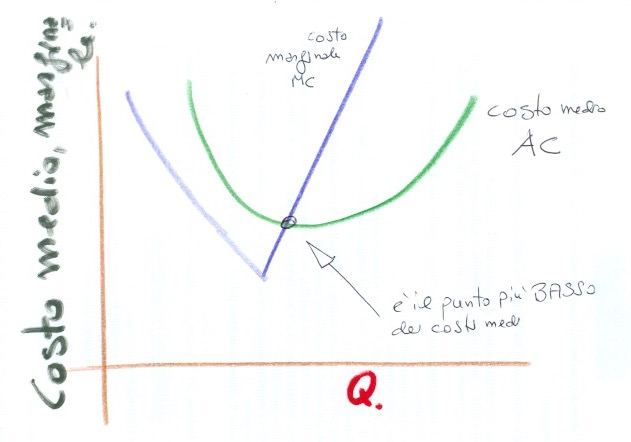
Si osservi come la curva di costo marginale colga quella dei costi medi nel punto più basso. Da quel punto in poi rappresenta anche la curva d’offerta. 

In realtà questa spiegazione non è completa; c’è una parte INFERIORE della curva d’offerta che dev’essere pur rappresentata! Ebbene si trova sull’ordinata finché è al di sotto del punto di contatto tra il marginale e quella di costo medio. S’osservi la seconda grafica proveniente dagli studi svolti presso l’Università Cattolica di Milano, slide 19 capitolo 8:

Chiarita la connessione tra costo marginale, costo medio e curva d’offerta, ora la fase 2 della soluzione al Micro problema.

La seconda regola da conosce e che emerge dal disegno è che in questo mercato, come si vede dal secondo disegno, il prezzo P è uguale al CM (costo marginale) e al costo medio (AC). Quindi ci serve il costo marginale.

Questo tipo di costo (il marginale) s’ottiene con la derivata prima del CT (costo totale).

Quindi se il CT = 10q al quadrato + 20 q

la derivata prima (ovvero il costo marginale) è 20q + 20

Ora serve il costo medio (AC) ovvero il CT/Q il che s’esprime, in questo esercizio con 10q + 20

Bene ora abbiamo sia il CM sia l’AC.

S’osservi la successione dei conteggi qui riportata: