Isoquanto birichino 2 come integrazione e completamento di quanto già pubblicato precedentemente sull’argomento il cui link di riferimento è posto in basso a questo studio.
C’è una diretta relazione tra la forma dei diversi isoquanti e il rendimento della produzione aziendale. Tale rendimento può essere del costante, crescente o decrescente.
Mi spiego meglio. L’isoquanto indicando il mix adeguato di fattori produttivi (due) da introdurre in produzione porta di conseguenza ad interrogarsi sulla resa del processo produttivo.
L’inserimento di materia prima nell’azione del produrre può portare l’output ad essere più che proporzionale a quanto inserito o meno che proporzionale. Può esserci anche il caso che tanto entra in lavorazione e tanto ne esce.
La connessione tra queste relazione d’inserimento di materia prima (rappresentate dall’isoquanto) produce tre sviluppi diversi nella mappa delle funzioni di produzioni possibili.
ATTENZIONE che qui sto usando le funzioni possibili come sinonimo di isoquanto per non ripetere la stessa parola più volte.
Nel caso ci trovassimo in una relazione di costanza tra inserimento di materia prima e prodotto finale la distanza tra un isoquanto e l’altra è costante. Si veda la grafica qui allegata.

Capito che il concetto è riassumibile nella distanza dall’origine dell’isoquanto tutto è a “scalare” e viene da se.
Ecco il caso di una produzione con rendimenti di scala crescenti. Anche qui si osservi come si riduce la distanza “b” con “a” e quindi “c”.

Infine il caso di rendimenti decrescenti qui rappresentati:
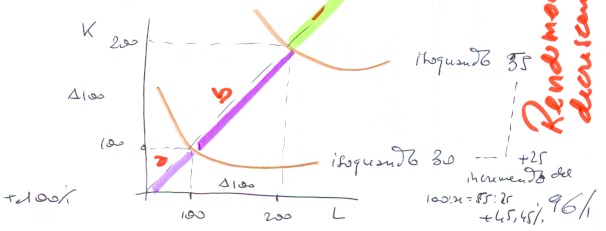
Questi passaggi sono molto importanti perchè aprono a un terzo ragionamento apparentemente complesso: la relazione tra la funzione di produzione e i rendimenti di scala.
L’argomento sarà trattato come terzo caso di studio per questa serie di analisi.
