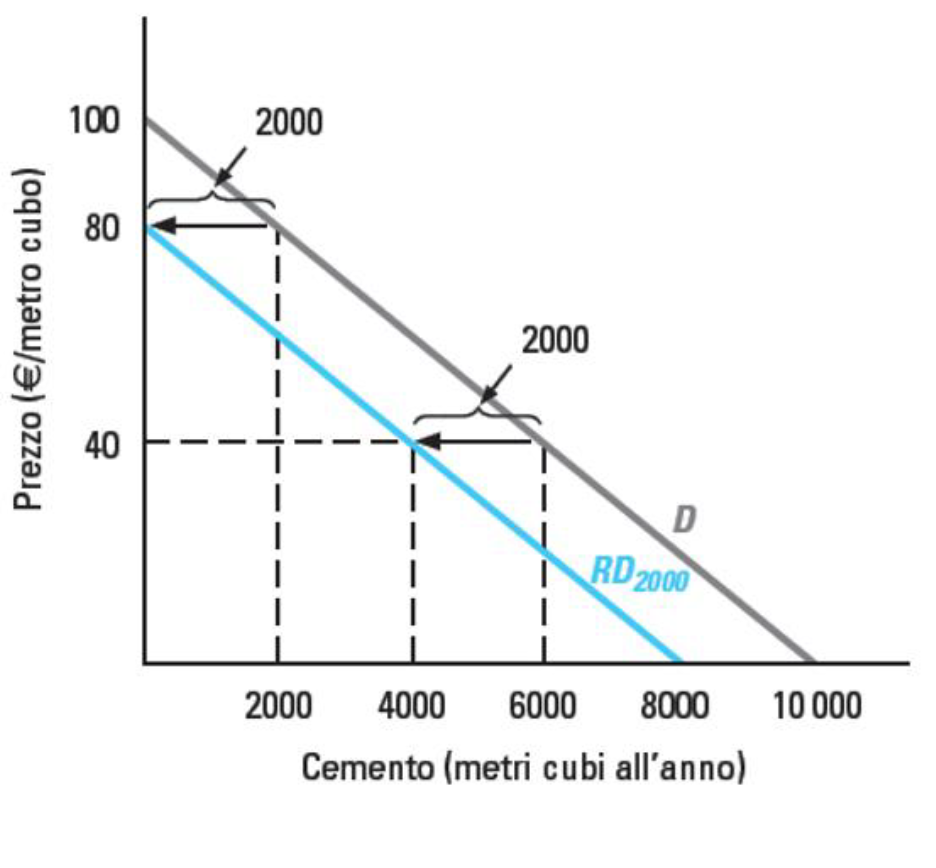
Funzione di domanda residuale secondo le specifiche dell’oligopolio pensato da Cournot (Antoine-Augustin Cournot, francese, matematico ed economista, 1801-1877).
L’argomento è apparentemente complesso. Spesso all’università viene “buttato là” dal docente lasciando lo studente con più dubbi che certezze. La missione di questo sito è “raccogliere i cocci e metterli insieme”.
Se siamo in un oligopolio ci troviamo con almeno 2 imprese che nel modello di Cournot si sono spartiti il mercato. Il problema è come se lo sono divisi, in parti uguali o a seconda del rispettivo peso di produzione?
Nella SITUAZIONE DI UNA DOMANDA RESIDUALE (è una delle possibilità) per ogni prezzo che si trova sul mercato, l’impresa A serve quella parte del mercato che non è già cliente di B e viceversa. Da questo “balletto” delle parti nasce il concetto di DOMANDA RESIDUALE e di conseguenza per calcolarla, l’annessa funzione.
Esprimendosi in altre parole a parità di concetto, la FUNZIONE DI DOMANDA RESIDUALE DELL’IMPRESA A spiega in corrispondenza alla quantità venduta dall’azienda B a quale prezzo A riesce a vendere la sua quantità Qa.
Fin qui siamo tutti in accordo (è facile), i dolori arrivano ora con i conti alla mano.
Sia data la funzione di domanda inversa (espressa per il prezzo) P = 100 – 0,01Q quindi i costi marginali pari a 40.
Trovandoci in oligopolio e applicando il concetto della domanda residuale è ovvio che la Q di mercato è pari a qa + qb quindi la funzione inversa di domanda è pari a P = 100 – 0,01qa – 0,01qb.
Dalla funzione di domanda diretta Q = 10.000 – 100P sappiamo che il mercato chiede 10mila pezzi. Quindi se l’impresa B produce 8.000 ne restano solo 2mila ad A.
S’osservi cosa accade adesso (magia). La quantità di 2mila pezzi per A la si cerca sull’ascissa, proiettandola quindi sulla domanda trovando così il prezzo di vendita (che diventa l’intercetta all’ordinata della funzione di domanda residuale.
Prego, si verifichi ciò sul grafico qui presente dove si rammenta anche il costo marginale pari a 40.
Il prezzo in ordinata pari a 80 non emerge solo dall’aver “tirato su” il tratteggiato dalla quantità prodotta fino ad impattare sulla curva di domanda complessiva di mercato e quindi la connessa proiezione sull’ordinata, ma dal calcolo della funzione di domanda residuale.
Si segua il conteggio.
P = (100 – 0,01 qa) – 0,01 qb
con un qa pari a 2.000 la funzione diventa:
P = 100 – 20 – 0,01 qb
ma 100 – 20 non fa 80?
Ecco svelato uno dei segreti del meccanismo, a seguire in un successivo studio altri passaggi d’approfondimento.