L’Isoquanto è una curva capace d’indicare LE DUE COMBINAZIONI (non è mai una sola!!!) che consentono d’ottenere lo stesso volume di produzione. Una tale dimensione viene sviluppata su un piano cartesiano. Generalmente ci sono più isoquanti tanti da formare una mappa di scelte.
Ecco l’isoquanto!

Fin qui nulla di strano senonchè abbiamo ben quattro forme diverse di isoquanto.
E’ possibile che i fattori della produzione siano perfetti sostituti; è il caso del gasolio con l’olio combustibile. Ne deriva che la forma dell’isoquanto cambia rispetto a quanto visto assomigliando alle curve d’indifferenza già studiate. Ecco la nuova forma:

C’è una terza forma di curva d’isoquanto che coglie quelle materie prime in produzione che sono complementari come le punte di trapano e il macchinario che le ospita. Ecco la connessa forma dell’isoquanto:

Alle tre forme di combinazione di fattori qui descritte, se ne aggiunge un’altra, la quarta, spesso trascurata dai libri di testo ma pretesa durante gli esami!
Si osservi la seguente funzione di produzione: f (x1, x2) = In (x1+1) + In (x2 + 1).
Tradotto in termini umani, In sta per isoquanto. Si legge: la funzione di produzione che utilizza due input (x1 e x2) si sviluppa su un isoquanto che ha un’intercetta all’ordinata e una all’ascissa.
Ecco la novità. Quel x1 + 1 vuol dire che la combinazione dei due input non resta sospesa nel piano cartesiano come osservato nel grafico 1 a questa relazione, bensì “impatta” con gli assi del piano.
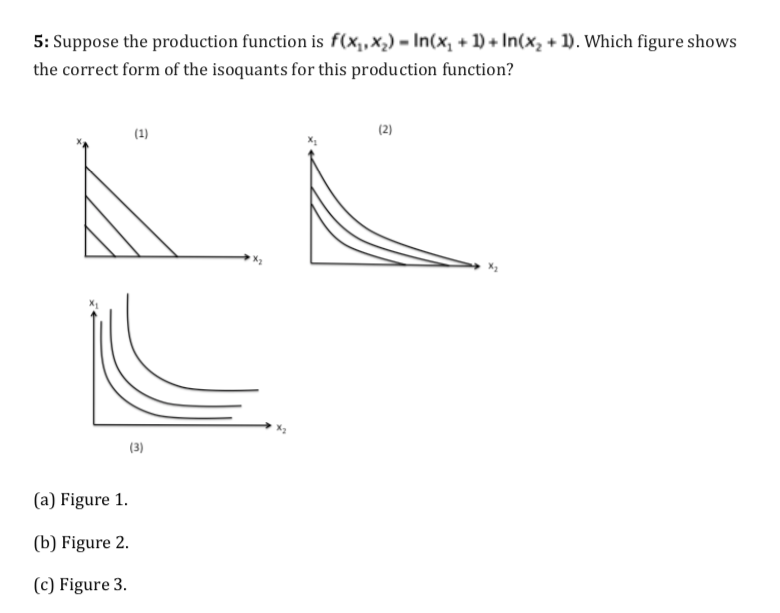
Solitamente una domanda di questo tipo è posta, nel tema d’esame, in termini grafici comparativi.
Vengono esposti 3 modelli di combinazione oltre alla funzione di produzione già indicata chiedendo allo studente di scegliere (identificare) quella corretta (la figura 2).
Chi non ha capito alzi la mano.
